Рубрика: просто блог

Очередной «вместолевый» эксперт делится откровениями о роли руководителей производств. Демонстрируя глубокое (по его мнению) понимание вопроса.

Душит смех.

Цирк, да и только.

Недавно мне удалось купить рюмки-стопки подходящего для меня размера. Объём одной стопки здесь 13 мл.

Это практически елабужская «муха». 🙂

Для тех, кто, как я, не «тренируется» пить крепкое регулярно, но тем не менее иногда позволяет себе — это идеальный объём. Организм отвык от больших объёмов и косеет невероятно быстро. А с такой рюмкой можно в обед под хорошую еду и употребить.

А я и не знал, что оказывается ещё и турбовинтовой самолёт делают.

Я тут внезапно обнаружил, что в составе kubuntu 24.04 LTS уже идёт Wayland.

Попробовал включил. Работает! Производительность графики, правда, с ним в 2 раза хуже, чем с X11, но мне в игры не надо играть.

Оставлю так. Посмотрим, как оно.

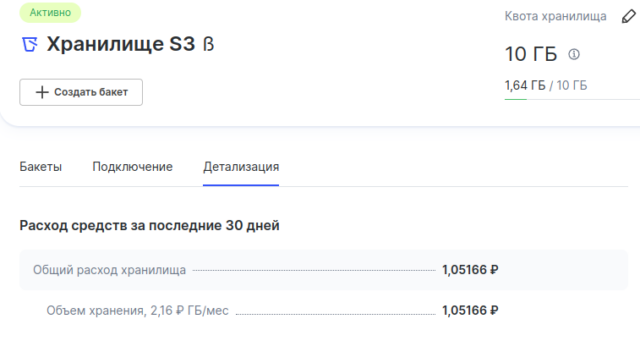
В качестве сервера синхронизации сейчас работает S3 хранилище (см. рис. 1). У рег.ру там сейчас, похоже, бета-тестирование сервиса, и они за S3 хранилище берут сущие копейки. Пишут, что со временем будут еще брать за трафик и за операции, но если расход мне покажется неприемлемым — существуют хорошие варианты от других провайдеров (например beget.com). Если что — без проблем уйду туда.

По степени защищенности от рисков этот вариант примерно равен «своему» виртуальному серверу, который хостится у того же провайдера.

Описанные ранее глюки мобильного клиента почему-то устранились указанием лимита на размер файлов в 10 Мб. Правда, время синхронизации мобилки занимает примерно пару минут. Это примерно то же самое, что было с Joplin при синхронизации через WebDAV. Это очень медленно, конечно (Joplin-сервер позволяет синхронизировать мобилку примерно за 3 секунды). Но приложения Обсидиана настолько хороши, что я даже готов смириться с мобильными тормозами, при условии, что не обнаружатся каких-нибудь критических недостатков в этом всём. (В этом случае уползу обратно на Joplin.)

P.S. Переезд на Obsidian потребовал некоторого колдунства над .md файлами, экспортированными из Joplin. Обошёлся двумя скриптами на perl и парой десятков ручных правок, которые оказалось быстрее сделать вручную чем писать еще один скрипт.

Был проведён эксперимент с синхронизацией копии моего хранилища в облако S3. Плагином Remotely Save.

С десктопной версией — успех. Мои 1.6 гигабайта туда залетают за 5 минут. И за те же 5 минут выгружаются на второй комп. Это практически мгновенно по сравнению с Joplin. Сама обычная синхронизация — быстрая. Пока не знаю насколько надёжная, конечно.

А вот с андроидной версией беда. Оно загрузило первые 1600 с хвостиком объектов и вылетело. И при последующих попытках синхронизации исправно вылетает (т.е. аварийно завершается) через каждые примерно 300-400 объектов. Каким-то образом тоненькие андроидные ножки у него заплетаются, и оно падает.

Из спортивного интереса попробую я андроидного обсидиана додрочить, чтобы он докачал всю базу. Даже интересно, хватит ли у меня терпения. За последний заход оно загрузило всего 92 объекта. Осталось примерно 4000. 🙂

P.S. Следующая попытка загрузила 46 объектов.

P.P.S. Проблема известна с 17 апреля 2023. Автро плагина «решил» проблему (и закрыл тикет) вот таким образом:

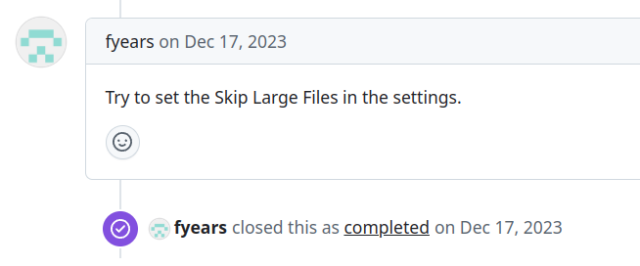
Маладэц!

Неделю назад я начал активно пользоваться Obsidian для хранения рабочих заметок.

По результатам недельного опыта его использования, уже могу сказать, что в Обсидиане отличный редактор текста заметок, да и вообще весь интерфейс приложения удобный. Это сделано заметно лучше, чем в Joplin.

Даже в некоторой степени завидую (как пользователь Joplin). Но персональные заметки я на Обсидиан пока не переведу, ибо штатная синхронизация Обсидиана — только через их сервер, и только за денежку. (Есть сторонние плагины для синхронизации «через что угодно», но доверия к ним я не испытываю.)

Продолжаю наблюдение.

Рутуб — говноплатформа.

Мало того, что они у себя сделали мусорку из видосов, супер-массово стыренных из ютуба и хаотично разбросанным по фальшивым каналам, так их сервера ещё и не вытягивают раздачу видосов 1080p на двойной скорости.

Это, прям, фу.

Бесит, когда хочешь сэкономить время на просмотр, а вместо этого пялишься на паузу при подгрузке очередного куска.

На рабочем компе вместо привычного нормального OneNote оказался установлен какой-то кастрированный «OneNote 10». Фу. Не нравится.

Начал я искать альтернативу среди того, что разрешено корпоративной политикой.

И нашел Obsidian. (Он разрешен в режиме работы с локальными файлами, без синхронизации с сервером.)

Оказался вполне годным заметочником с хорошим поиском.

В общем, вот.